↓bottom↓
il TEOREMA di GAUSS per il CAMPO ELETTRICO
 ...
...
una premessa: il problema del piccolo Gauss sulla somma dei numeri da 1 a 100
la chiave per la soluzione è la "simmetria" e sarà la chiave anche per risolvere il Teorema di Gauss per il campo elettrico...
1. vettore area
si definisce il vettore AREA di una superficie piana il vettore che ha:
- MODULO pari alla area della superficie
- DIREZIONE perpendicolare alla superficie
- VERSO arbitrario se la superficie è aperta e uscente dalla superficie se questa è chiusa
 visualizzazione del vettore area: https://www.geogebra.org/m/GtgBUcGN (geogebra link)
visualizzazione del vettore area: https://www.geogebra.org/m/GtgBUcGN (geogebra link)
2. prodotto scalare
 richiami di matematica: il PRODOTTO SCALARE
richiami di matematica: il PRODOTTO SCALARE
3. FLUSSO di un VETTORE
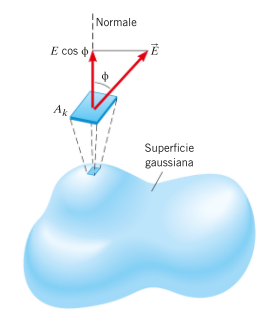
si definisce FLUSSO di un VETTORE attraverso una superficie piana, il prodotto scalare:
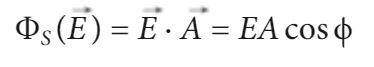
 flusso del campo elettrico: https://www.geogebra.org/m/pYR2t8FN (geogebra link)
flusso del campo elettrico: https://www.geogebra.org/m/pYR2t8FN (geogebra link)
4. FLUSSO di un VETTORE attraverso una superficie chiusa o superficie GAUSSIANA
- si divide la superfcie gaussiana in k parti ciascuna delle quali sia abbastanza piccola da poter essere considerata PIANA e tale che il campo elettrico su di essa possa essere considerato UNIFORME, ad esempio come nella sfera stroboscopica
si definisce FLUSSO di un VETTORE attraverso una superficie GAUSSIANA, la somma di tutti i prodotti scalari attraverso ciascuna superficie piana in cui è stata suddivisa la superficie gaussiana:
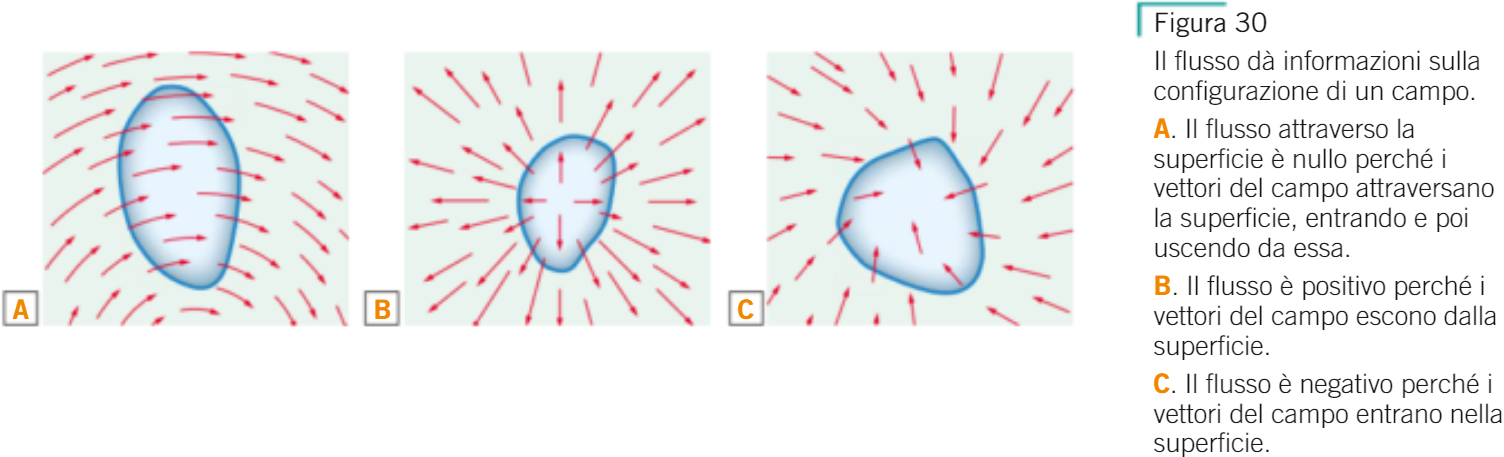
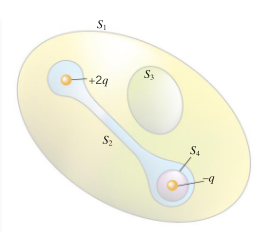
in figura B, all'interno della superficie c'è una "sorgente"
in figura C, all'interno della superficie c'è un"pozzo"
5. Il Teorema di Gauss per il campo elettrico:
ma come fare a sommare tantissimi prodotti scalari?
la soluzione la fornisce GAUSS che da bambino sapeva sommare tanti numeri naturali!!!!
costante dielettrica nel vuoto
ε0=8,85·10-12 C2/Nm2
VideoLezione: Il Teorema di Gauss per il campo Elettrico:
Applicazioni del Teorema di GAUSS per il campo elettrico
un'applicazione del teorema di Gauss:
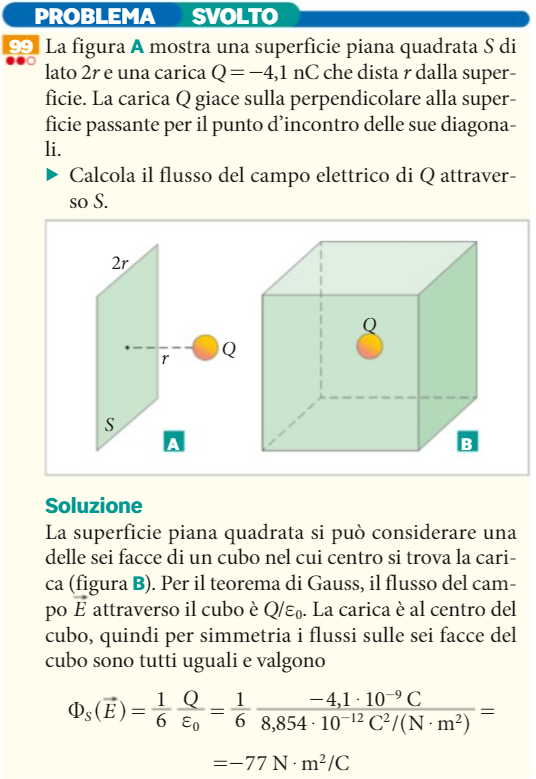
Il teorema di Gauss e la legge di Coulomb
Il teorema di Gauss e la legge di Coulomb esprimono in modi diversi la stessa proprietà dell’interazione elettrostatica.
Si può infatti dimostrare che le due leggi sono equivalenti.
Ciò significa che a partire dal primo si può derivare la seconda e viceversa.
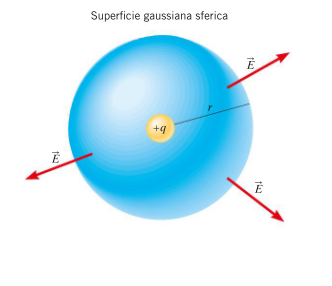
Vediamo solo come dal teorema di Gauss si possa ricavare la legge di Coulomb calcolando il flusso del campo elettrico generato da una carica puntiforme q attraverso una superficie gaussiana sferica con centro la carica q
....vd. pag.133-134....
una applicazione del teorema di Gauss: n.105 pag.159
SOLUZIONE n.105 pag.159 (png)
 OLD Soluzione n.55 pag.653 (pdf)
OLD Soluzione n.55 pag.653 (pdf)
Campi Elettrici generati da distribuzioni di carica SIMMETRICHE
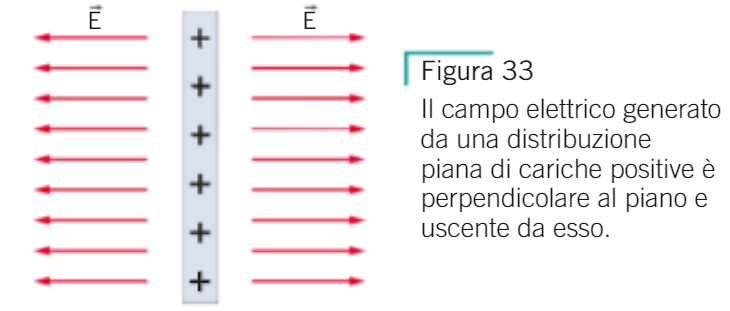
1. il campo elettrico generato da un PIANO UNIFORMEMENTE CARICO
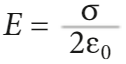
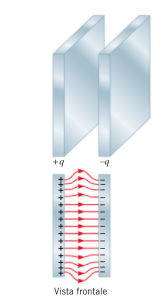
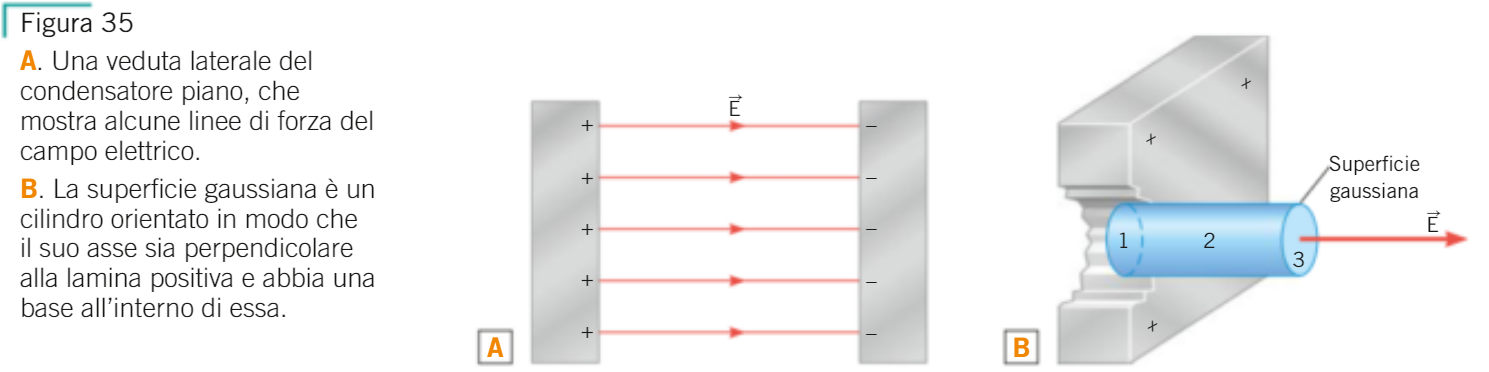
2. il campo elettrico generato da un CONDENSATORE PIANO:
Un condensatore piano è un dispositivo formato da due lamine metalliche parallele di uguale area, dette armature
Un condensatore si carica ponendo una carica positiva +q su un’armatura e una carica negativa -q sull’altra armatura
il CAMPO ELETTRICO all'interno di un condensatore piano è uniforme
per semplicità si trascurano gli "effetti di bordo" rappresentati nella figura sopra
 simulazione di un CONDENSATORE piano intro (link)
simulazione di un CONDENSATORE piano intro (link)
Il flusso elettrico attraverso l’intera superficie gaussiana è la somma dei tre flussi calcolati
- il flusso attraverso la superficie 1 è nullo perchè si ha E=0 all'interno del conduttore
- il flusso attraverso la superficie 2 è nullo perchè E·A·cos(90°)=E·A·0=0
- il flusso attraverso la superficie 3 vale E·A·cos(0°)=E·A
Per il teorema di Gauss, il flusso elettrico è uguale a Q/e0, dove Q è la carica totale all’interno del cilindro gaussiano, segue:
E·A = Q/e0
oppure, detta σ la densità superficiale di carica Q/A
E = σ/ε0
- - - - - - - - -
Potevamo giungere allo stesso risultato utilizzando il principio di sovrapposizione e considerando le armature come due configurazioni piane infinite uni- formemente cariche aventi la stessa densità superficiale di carica, ma con segno opposto
Ripasso: Campo elettrico del condensatore
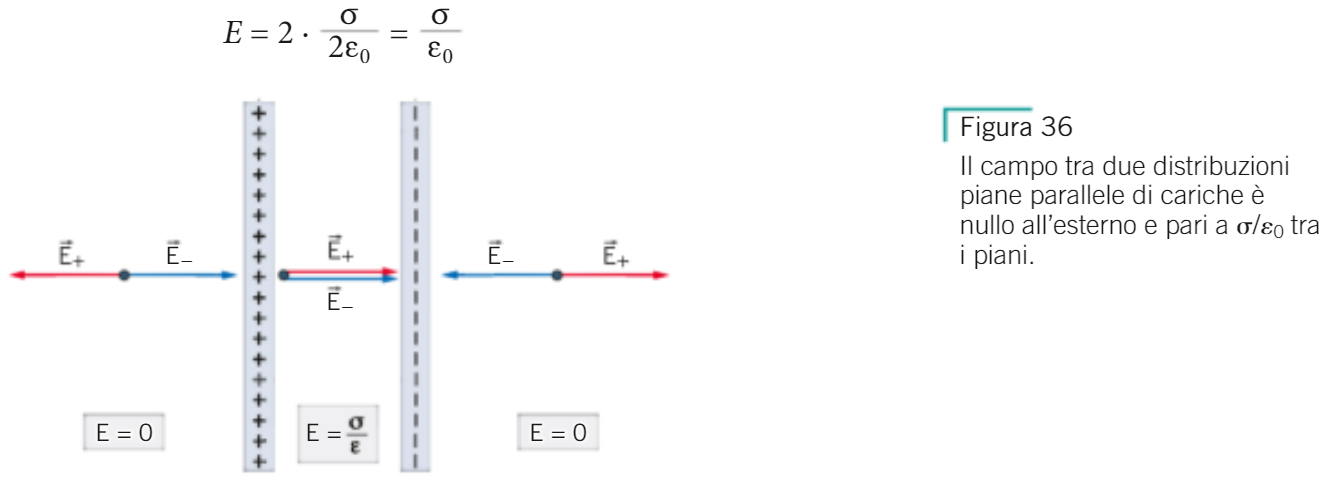
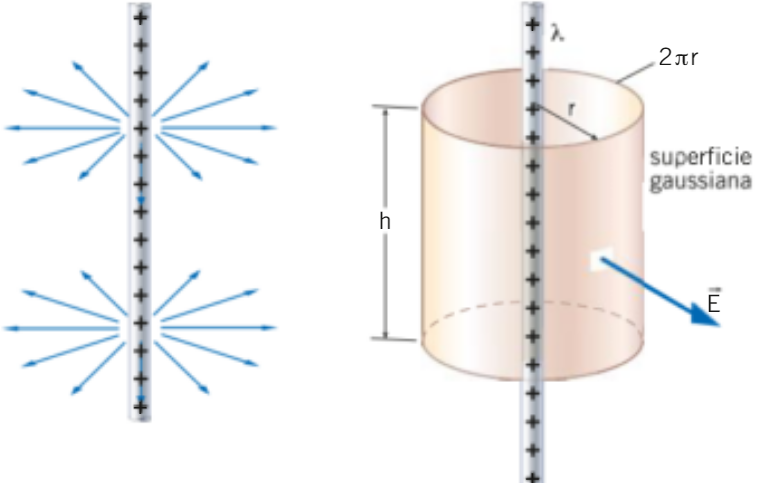
3. il campo elettrico generato da un FILO UNIFORMEMENTE CARICO:
conviene scegliere come superficie gaussiana un cilindro coassiale al filo
- il flusso attraverso le due aree di base è nullo perchè E·A·cos(90°)=E·A·0=0
- il flusso attraverso la superficie laterale vale E·Asup.later.=E·2π·r·h
Per il teorema di Gauss, il flusso elettrico è uguale a Q/ε0, dove Q è la carica totale sul filo all’interno del cilindro gaussiano, segue:
E·2π·r·h = Q/ε0
oppure, detta λ la densità lineare di carica Q/h
E = λ/(2π·r·ε0)
il campo elettrico non è uniforme e il suo modulo risulta inversamente proporzionale alla distanza dal filo
- - -
RIPASSO e approfondimento: Il campo elettrico generato da un filo uniformemente carico (POLIMI)
Esercizi svolti
Flusso del campo elettrico e teorema di Gauss: problemi - Campo elettrico p.9
...per ora finisce qui, ma.... tenetevi pronti per il quinto anno...
il TEOREMA di GAUSS per il CAMPO MAGNETICO
 ...
...

il flusso del campo magnetico si misura in Wb
una UNITA' di MISURA per il flusso magnetico: il weber
[Wb] = [T·m²]
in onore di Wilhelm Eduard WEBER (De, 1804-1891)
 ...
...
coraggio... manca una ultima unità di misura....
questa equazione esprime matematicamente il fatto che:
1 - NON esistono monopoli magnetici
ossia ogni superficie gaussiana raccoglie sempre un ugual numero di poli N e poli S
QUINDI le "sorgenti di campo magnetico NON solo i poli magnetici
APPROFONDIMENTO: Quest for the curious magnetic monopole continues (CERN) 
2 - le linee di forza del campo magnetico B sono sempre LINEE CHIUSE
ossia ogni superficie gaussiana è attraversata sempre da un ugual numero di linee di forza entranti ed uscenti
NON ci sono sorgenti e pozzi (vd figura A per il campo elettrico)
- - -
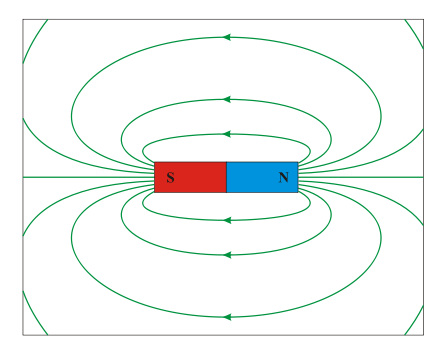
Linee di forza del campo magnetico
Sono sempre linee chiuse!!!
anche se in queste figure non si evince...
Linee di campo magnetico generate da un magnete |
Linee di campo magnetico generate da una spira circolare percorsa da corrente |
Linee di campo magnetico generate da un solenoide percorso da corrente |
|
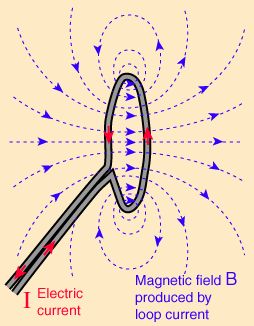 al centro della spira: B=µ0·I / (2R) |
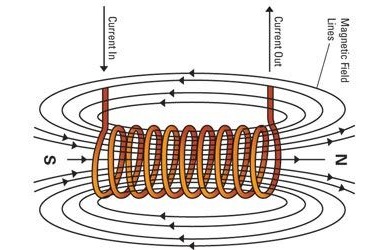 all'interno del solenoide: B=µ0·N· I / L |
ripasso e approfondimento
Campo magnetico e teorema di Gauss - parte1 (Davide Contini)
Campo magnetico e teorema di Gauss - parte2 (Davide Contini)
↑top↑

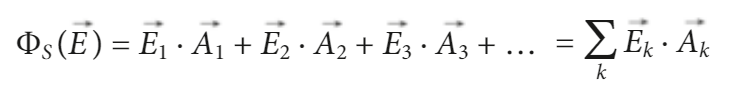



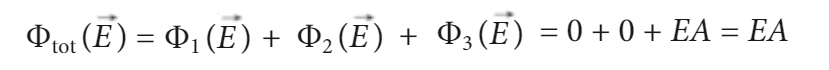
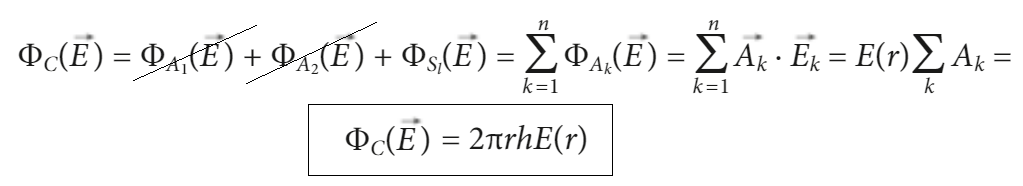
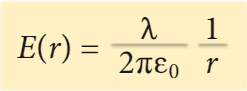
 ???
???