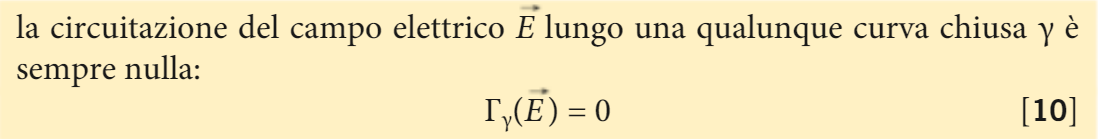↓bottom↓

il TEOREMA di AMPÉRE per il CAMPO ELETTRICO e MAGNETICO

...

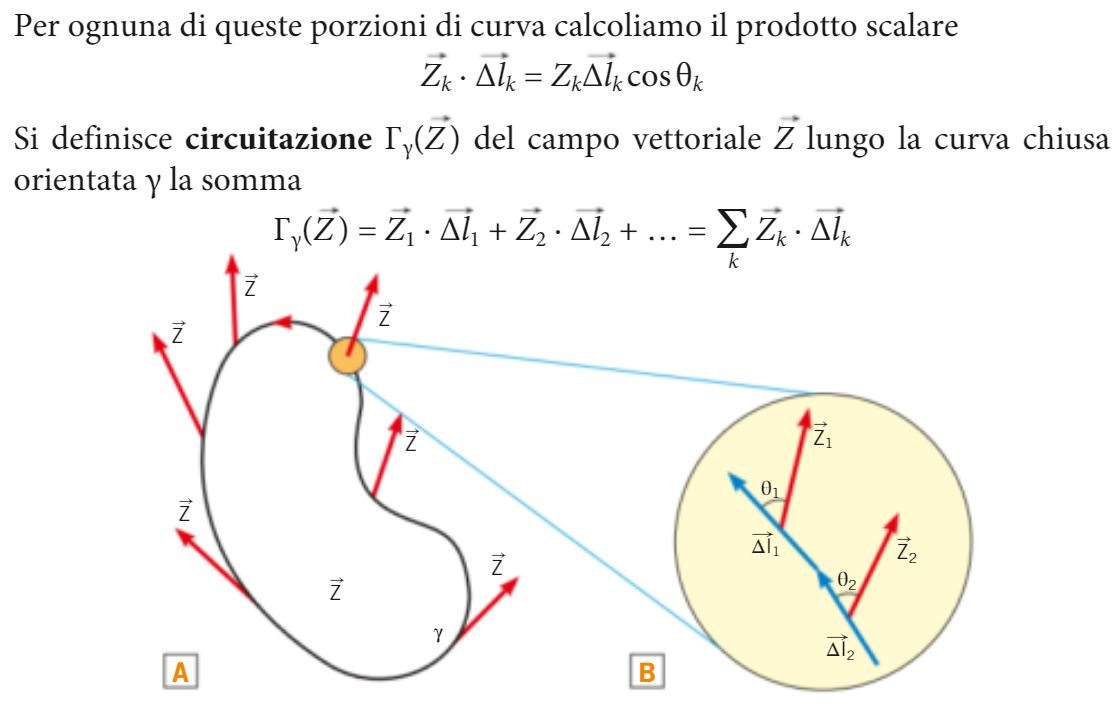
premessa: la circuitazione di un campo vettoriale:

La circuitazione di un campo vettoriale. Cos'è IN CONCRETO

richiami di matematica: il PRODOTTO SCALARE

il TEOREMA di AMPÉRE per il CAMPO ELETTRICO

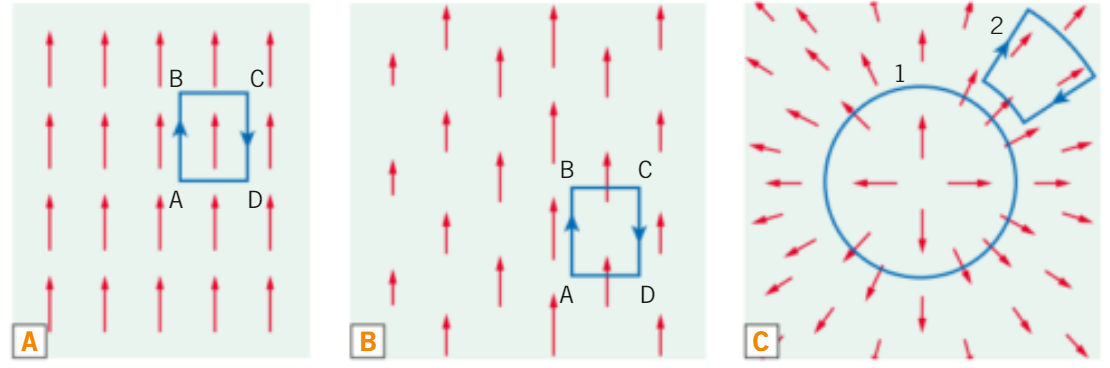
alcuni esempi di circuitazione del campo elettrostatico:

questa equazione esprime matematicamente il fatto che:

1 - il campo E è un campo conservativo

ossia ogni curva chiusa γ parte e ritorna ad un punto con lo stesso potenziale elettrico

2 - e si può definire una energia potenziale elettrica
(come già fatto per il campo gravitazionale)

ossia ad ogni punto del campo ELETTROSTATICO posso associare un valore del potenziale elettrico V

- - -

Approfondimento

Ma Perché un Campo Conservativo deve essere Irrotazionale?

ok, c'è tanta matematica da fare.... per ora ci si deve accontentare...

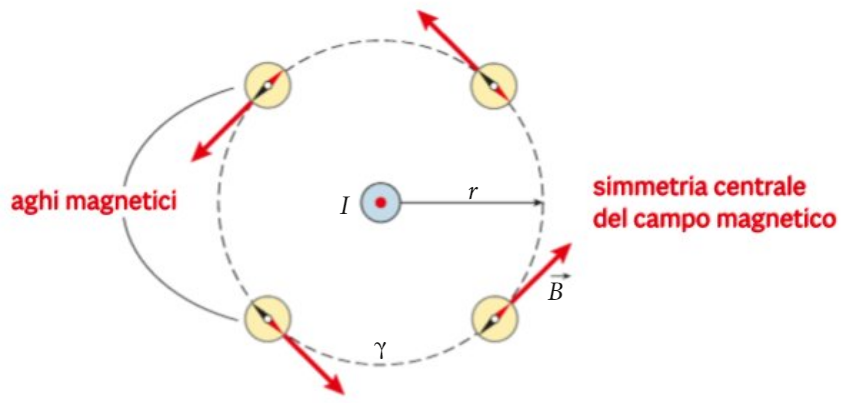
il TEOREMA di AMPÉRE per il CAMPO MAGNETICO

questa equazione esprime matematicamente il fatto che:

1 - il campo B NON è un campo conservativo

ossia le correnti elettriche sono sorgenti di campo magnetico

2 - NON si può definire una energia potenziale magnetica

ossia ad ogni punto del campo magnetico NON posso associare un valore di un potenziale

Applicazioni

3 - applicando il Teorema di Ampère si può ricavare la legge empirica di Biot e Savart

(vd.esempio 8 pag.306)

dal Teorma di Ampère segue la legge di Biot-Savart(Cristian Manzoni POLIMI)

4 - applicando il Teorema di Ampère si può calcolare il campo magnetico all'interno di un SOLENOIDE

(vd.pag.307-308)

B=µ₀·N· I / L

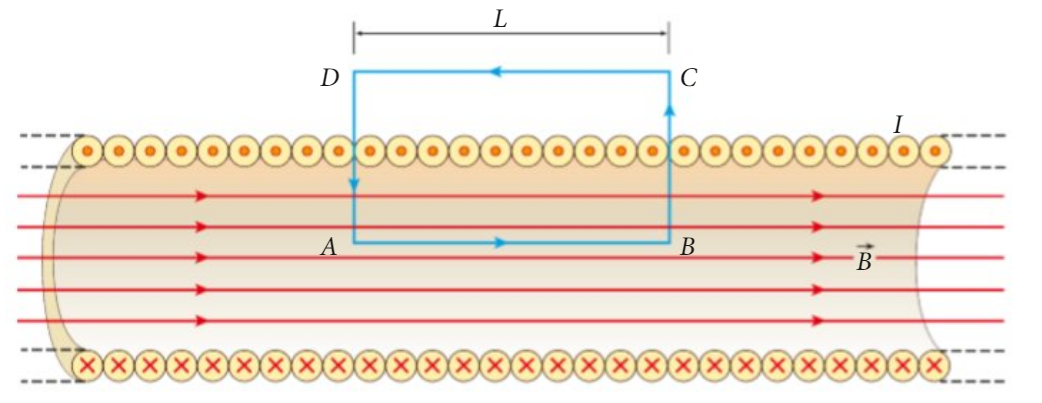
Teorema di Ampère per il campo magnetico B (Davide Contini POLIMI)

Ripasso e Approfondimenti

Circuitazione del campo magnetico e teorema di Ampere

↑top↑